發(fā)布日期：2025-5-9 11:15:17
1、引言
損傷容限評估方法已成為航空發(fā)動機(jī)壽命限制件的設(shè)計(jì)與服役管理的核心內(nèi)容，其中轉(zhuǎn)子部件裂紋擴(kuò)展壽命的準(zhǔn)確預(yù)測是損傷容限評估的關(guān)鍵環(huán)節(jié)[1-3]。與標(biāo)準(zhǔn)緊湊拉伸（CT）試樣中的穿透型初始裂紋不同，轉(zhuǎn)子壽命限制件的初始裂紋往往萌生于機(jī)械加工導(dǎo)致的表面缺陷或者冶金過程引入的內(nèi)部缺陷，具有一定的三維形貌特征。對于發(fā)動機(jī)輪盤中的典型半圓形埋入表面裂紋，從裂紋前緣與輪盤表面的交點(diǎn)到裂紋前緣最深點(diǎn)，應(yīng)力狀態(tài)由近平面應(yīng)力狀態(tài)逐漸轉(zhuǎn)變?yōu)榻矫鎽?yīng)變狀態(tài)，而這種裂紋前緣不同位置應(yīng)力狀態(tài)的不同，會引起裂紋尖端微小區(qū)域約束效應(yīng)（又稱拘束度）的不同，進(jìn)而導(dǎo)致裂紋擴(kuò)展有效驅(qū)動力不同[4-7]。在分析表面疲勞裂紋擴(kuò)展問題時，考慮裂紋前緣不同位置的三維約束效應(yīng)可以建立更為準(zhǔn)確的裂紋擴(kuò)展模型，進(jìn)而評估轉(zhuǎn)子壽命限制件的損傷容限性能，支撐發(fā)動機(jī)安全設(shè)計(jì)與服役管理。
求解裂尖約束效應(yīng)的基礎(chǔ)是建立能夠準(zhǔn)確描述裂尖應(yīng)力應(yīng)變場分布的方法�；诰�彈性條件下的裂尖區(qū)域應(yīng)力強(qiáng)度因子K場或彈塑性條件下裂尖HRR（Hutchinson-RiceRosengreen）解，學(xué)者們提出了包括K-T、J-Q、K-T-Tz、J-T、J-A2、J-Q-Tz等雙參數(shù)、三參數(shù)描述方法[8-12]。Williams等[13]首先建立了裂尖應(yīng)力場K-T雙參數(shù)描述，使用非奇異T應(yīng)力提高K的描述精度，并反映面內(nèi)約束，O'Dowd等使用Q參數(shù)來反映彈塑性條件下裂紋面內(nèi)的約束效應(yīng)[14]。在描述面內(nèi)約束的T、Q參數(shù)基礎(chǔ)上，郭萬林[15]引入了離面約束因子Tz表征面外約束效應(yīng)，以更全面反映三維裂紋體尖端的應(yīng)力狀態(tài)。于培師等[16-17]分析了不同構(gòu)件的角裂紋、表面裂紋等三維裂紋前緣不同位置處的Tz分布，并提出將裂紋前緣的Tz分布等效為不同厚度板內(nèi)中心穿透裂紋前緣的Tz分布。趙軍華等[18]基于Tz提出考慮面外約束的K-Tz雙參數(shù)理論。為了結(jié)合面內(nèi)約束和面外約束的影響，郭萬林等[19]進(jìn)一步提出了K-T-Tz、J-Q-Tz等三參數(shù)理論描述裂紋前緣三維應(yīng)力場，并通過對比K-T、J-Q分析結(jié)果，指出三參數(shù)理論能更準(zhǔn)確地解釋三維應(yīng)力場。
鑒于三參數(shù)方法對裂尖應(yīng)力場描述的復(fù)雜性，一種思路是構(gòu)建一個綜合性參數(shù)作為約束效應(yīng)的表征參數(shù)，Mostafavi等[20]使用當(dāng)前裂尖塑性區(qū)的面積與高約束作用下裂尖塑性區(qū)面積比值φ來表征裂尖約束效應(yīng)，該參數(shù)不適用于大范圍屈服情況。楊杰等[21]提出了一個基于裂尖等效塑性應(yīng)變面積的統(tǒng)一約束因子，綜合反映裂尖面內(nèi)和面外的約束效應(yīng)�？紤]到塑性應(yīng)變面積計(jì)算的復(fù)雜性，徐建勇等[22]進(jìn)一步使用裂尖張開位移比值作為綜合約束因子。然而上述研究多用于裂紋體的斷裂韌性研究，針對不同約束作用下的裂紋擴(kuò)展研究，Newman[23]首先在條帶屈服模型基礎(chǔ)上引入裂尖約束因子，將其定義為最大主應(yīng)力與屈服應(yīng)力之比，指出金屬材料平面應(yīng)力和平面應(yīng)變狀態(tài)下的約束因子分別為1和3。Machniewicz等[24]指出，裂紋張開時裂尖前方塑性區(qū)內(nèi)不同位置的約束因子呈拋物線型分布。Newman等[25]通過數(shù)學(xué)處理給出了裂尖前方平均約束因子，指出其會隨裂紋加載情況、裂紋體厚度和裂尖塑性區(qū)大小發(fā)生變化。Daniewicz[4]使用應(yīng)力強(qiáng)度因子切片合成方法近似計(jì)算三維表面裂紋的裂紋面位移和裂尖塑性區(qū)尺寸。郭萬林等[26]、Wang等[27]和McMaster等[28]分別給出了約束因子的經(jīng)驗(yàn)公式。吳連生等[29]、許磊[30]、周斌[31]利用約束因子預(yù)測了不同厚度穿透裂紋和表面裂紋的裂紋擴(kuò)展速率。這些模型或者求解復(fù)雜或者需要基于試驗(yàn)數(shù)據(jù)擬合，如何快速、準(zhǔn)確計(jì)算不同載荷和厚度下的裂尖三維約束因子，成為裂紋擴(kuò)展預(yù)測的關(guān)鍵因素之一。
隨著有限元技術(shù)的不斷發(fā)展，結(jié)合數(shù)據(jù)分析程序進(jìn)行聯(lián)合仿真，為三維裂紋前緣不同位置處拉伸塑性區(qū)和變約束因子的計(jì)算提供了有力手段。本文將采用Newman提出的約束因子描述裂紋前緣約束程度，以TC4鈦合金表面裂紋小尺寸試樣為研究對象，構(gòu)建裂紋前緣不同位置約束因子快速計(jì)算方法，獲得約束因子隨外加載荷、裂紋尺寸以及裂紋形狀的變化規(guī)律，并與傳統(tǒng)的計(jì)算模型進(jìn)行對比。
2、分析方法
2.1表面裂紋試樣有限元模型
本文所研究材料為直接從發(fā)動機(jī)風(fēng)扇盤中心孔區(qū)域取樣的TC4鈦合金。為確保該材料的各項(xiàng)同性特征，為后續(xù)三維約束因子計(jì)算提供支撐，從周向（CD）、徑向（RD）和軸向（AD）三個方向分別取樣，并進(jìn)行金相分析、硬度測試和拉伸試驗(yàn)。圖1給出了TC4合金的三維顯微組織，各方向上均呈現(xiàn)出典型等軸組織特征，平均晶粒尺寸分別為21.6μm、21.8μm和23.1μm，基本一致。三個方向維氏硬度測量結(jié)果分別為316HV、324HV和321HV，呈現(xiàn)出與組織一樣的均勻性特征[32]。
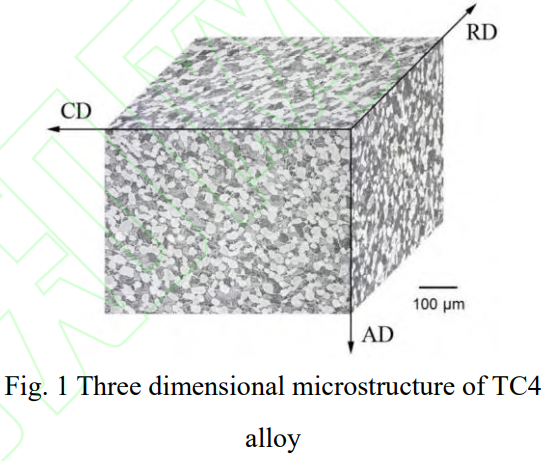
圖2為TC4鈦合金三個方向的拉伸曲線，三個方向拉伸性能差異較小，結(jié)合組織和硬度測試結(jié)果，表明本研究所用TC4鈦合金材料具有各向同性特征，為后續(xù)表面裂紋三維彈塑性應(yīng)力場分析和約束因子計(jì)算提供了支撐。采用彈塑性Ramberg-Osgood模型描述拉伸曲線：
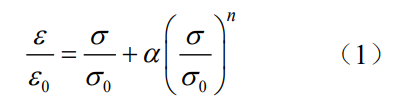
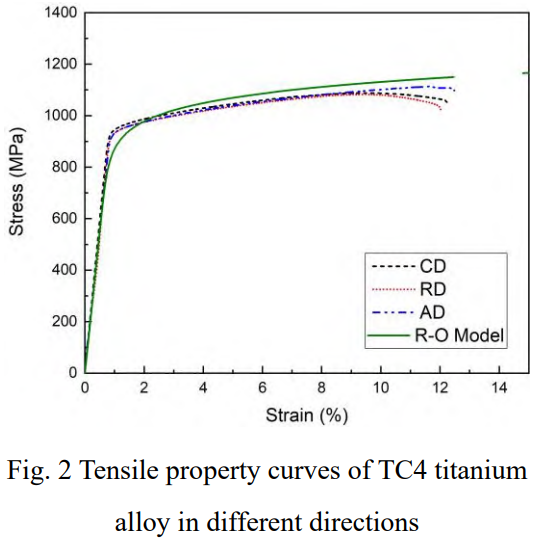
式中，ε0=σ0/E，屈服強(qiáng)度σ0=960MPa，彈性模量E=110GPa，參數(shù)α=0.227，n=14.33。
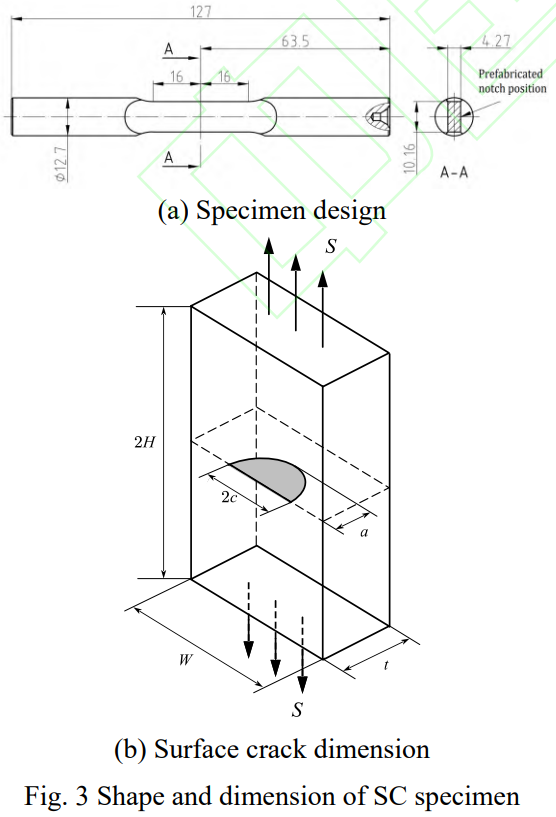
參考文獻(xiàn)[33]中表面裂紋（surfacecrack，SC）試樣尺寸并考慮疲勞試驗(yàn)機(jī)實(shí)際夾持要求，設(shè)計(jì)圖3所示SC試樣，其中夾持段為Φ12.7mm圓棒，標(biāo)距段為43.38mm2的矩形截面。在標(biāo)距段中間位置置入表面裂紋如圖3（b）所示，其中半軸長分別為a和c，試樣厚度為t，遠(yuǎn)端外加應(yīng)力為S。考慮到試樣對稱性，選取試樣中段的1/4部分進(jìn)行有限元建模，并保證加載面和邊界條件不影響表面裂紋周圍應(yīng)力場。
保持試樣尺寸不變，設(shè)定不同的裂紋深度比a/t、裂紋半軸比a/c以及加載應(yīng)力S/σ0，以研究不同裂紋尺寸、形狀以及外加載荷水平下的約束效應(yīng)，具體取值如下：a/t=0.05，0.1，0.2，0.4，0.6；a/c=0.75，0.9，1，1.1，1.25，1.4，1.55；S/σ0=0.45，0.5，0.54，0.59。對上述參數(shù)進(jìn)行組合計(jì)算，累積共5×7×4=140個算例。
2.2自適應(yīng)程序化網(wǎng)格生成方法
考慮到算例較多，建立自適應(yīng)程序化表面裂紋試樣單元設(shè)置和網(wǎng)格劃分流程，實(shí)現(xiàn)不同算例網(wǎng)格模型的快速構(gòu)建，具體步驟為：
（1）求解表面裂紋應(yīng)力強(qiáng)度因子Kmax。利用公式（2）估算表面裂紋在表面點(diǎn)和最深點(diǎn)處裂紋面內(nèi)的塑性區(qū)尺寸rp，其中表面點(diǎn)和最深點(diǎn)處的約束因子α分別取為1和3。
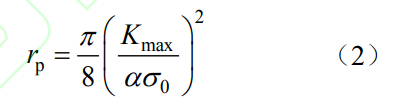
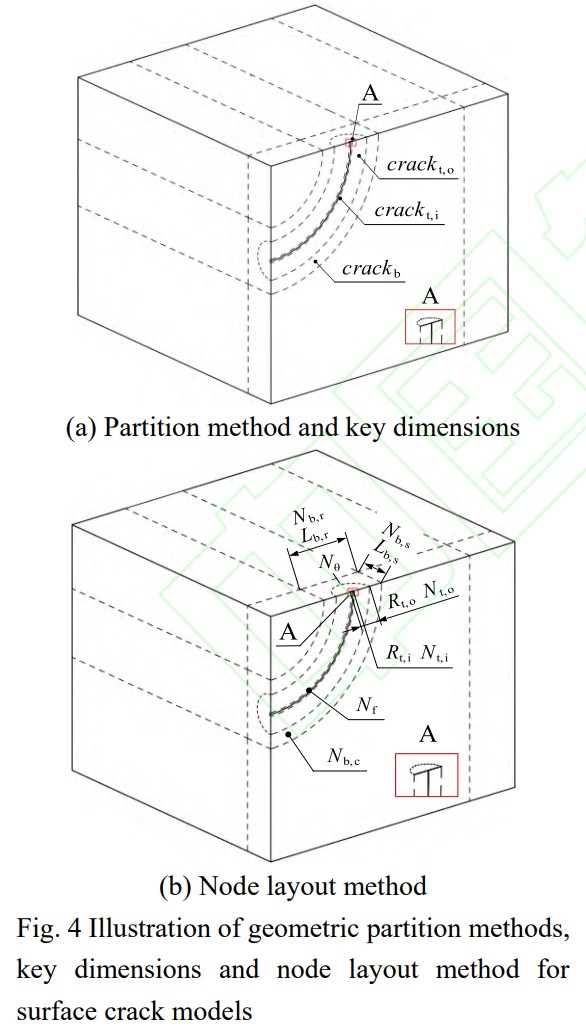
（2）將裂紋前緣線周圍空間分割為管狀區(qū)域以便于網(wǎng)格劃分。將該管狀區(qū)域分為內(nèi)管狀域crackt,i和外管狀域crackt,o，對應(yīng)的半徑分別為Rt,i和Rt,o。對Rt,i和Rt,o進(jìn)行賦值使得裂紋前緣最小塑性區(qū)尺寸rp,min≥Rt,i且最大塑性區(qū)尺寸rp,max≤Rt,o。
（3）在管狀域外圍劃分過渡域crackb作為網(wǎng)格過渡區(qū)域。設(shè)定該過渡域的截面尺寸為Lb,r≈2Rt,o，Lbox,s≈2Rt,o。
（4）按上述方法和尺寸要求，對含表面裂紋的幾何模型進(jìn)行分割，分割后的實(shí)體均可劃分六面體網(wǎng)格。含表面裂紋幾何模型的分割方式、局部關(guān)鍵尺寸如圖4（a）所示。
（5）設(shè)定裂紋前緣節(jié)點(diǎn)數(shù)Nf和過渡域crackb外側(cè)節(jié)點(diǎn)數(shù)Nb,c。為了保證過渡域中網(wǎng)格從裂紋前緣一側(cè)到無裂紋一側(cè)能夠順利過渡，一般設(shè)定Nb,c=Nf/3。
（6）設(shè)定內(nèi)管狀域crackt,i和外管狀域crackt,o的截面徑向節(jié)點(diǎn)數(shù)目Nt,i和Nt,o，以及周向節(jié)點(diǎn)數(shù)目Nθ，以保證塑性區(qū)有足夠的網(wǎng)格數(shù)。同時為了確定合適的網(wǎng)格尺寸以保證計(jì)算結(jié)果的準(zhǔn)確性，對裂尖前方不同網(wǎng)格密度的有限元模型進(jìn)行多次試算發(fā)現(xiàn)，當(dāng)裂尖前方塑性區(qū)內(nèi)網(wǎng)格數(shù)目在10個以上時，最終計(jì)算的約束因子數(shù)值變化在1%以內(nèi)，該結(jié)果與Daniewicz等[34]研究一致。本文設(shè)定周向節(jié)點(diǎn)數(shù)Nθ=16，確保塑性區(qū)內(nèi)至少包含10個單元。
（7）利用管狀域截面徑向和周向結(jié)點(diǎn)進(jìn)行管狀域截面的網(wǎng)格劃分，然后通過掃掠方式沿裂紋前緣曲線實(shí)現(xiàn)裂紋前緣方向管狀域的整體網(wǎng)格劃分。截面網(wǎng)格與裂紋前緣曲線垂直，保證每個裂紋前緣位置處截面網(wǎng)格均為圍繞裂紋尖端的同心環(huán)形分布。
（8）設(shè)定過渡域crackb的截面節(jié)點(diǎn)數(shù)分別為Nb,r≈8，Nb,s≈4，合理設(shè)定其余實(shí)體的網(wǎng)格節(jié)點(diǎn)數(shù)以保證單元尺寸過渡平順。
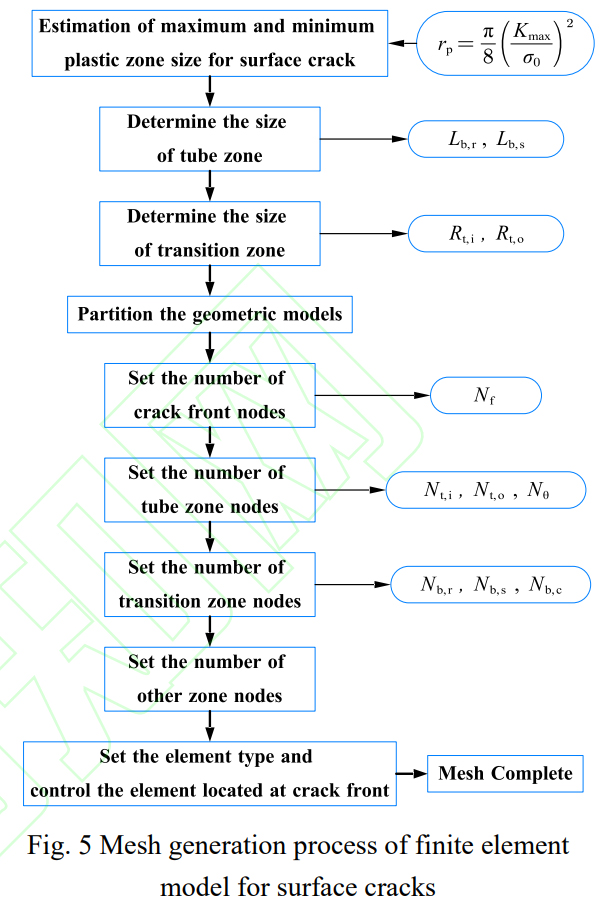
（9）使用六面體二次減縮積分單元對全部有限元實(shí)體進(jìn)行網(wǎng)格劃分，保證網(wǎng)格質(zhì)量滿足彈塑性分析要求。將與裂紋前緣相連的單元面坍縮為裂紋前緣上的線段，坍縮到同一位置的節(jié)點(diǎn)并不會縮并為一個節(jié)點(diǎn)，在后續(xù)加載過程中各節(jié)點(diǎn)仍可自由移動。這樣處理能近似取得裂紋前緣接觸單元內(nèi)應(yīng)變r-1的漸近趨勢。圖5給出了表面裂紋試樣程序化網(wǎng)格劃分流程。
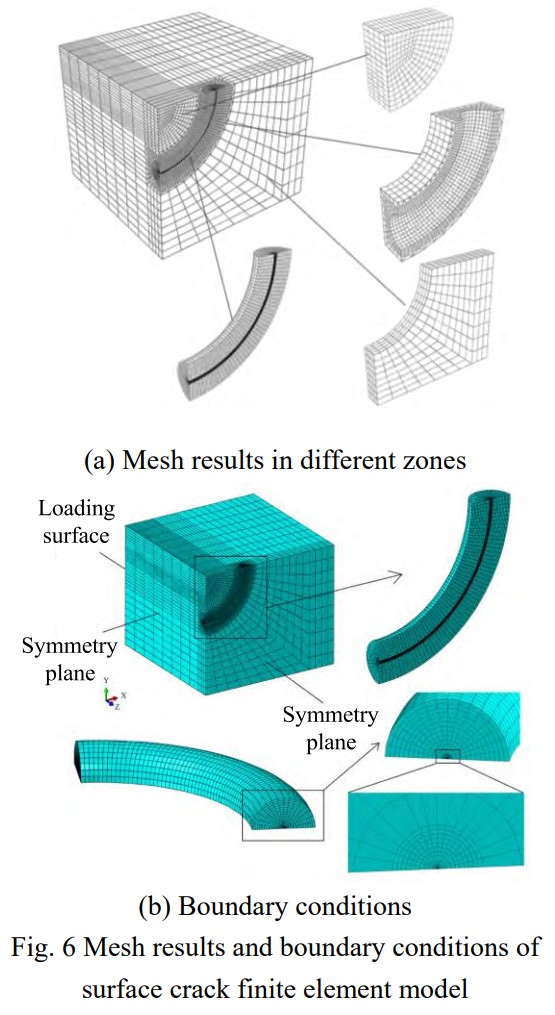
通過Abaquspythonscript前處理腳本對所有表面裂紋算例進(jìn)行網(wǎng)格劃分。圖6（a）為表面裂紋不同區(qū)域網(wǎng)格劃分情況，可見所有區(qū)域均可由六面體單元組成，網(wǎng)格由裂紋區(qū)的密集分布逐漸過渡到試樣表面的相對稀疏狀態(tài)。圖6（b）給出了最終的網(wǎng)格模型和邊界條件，在模型端面施加軸向拉伸載荷，在對稱面施加對稱邊界條件。
2.3裂紋前緣三維約束因子計(jì)算
在Newman等基于條帶屈服模型的約束效應(yīng)研究中，約束因子α通�；谌S彈塑性有限元分析的裂尖塑性區(qū)內(nèi)應(yīng)力分布進(jìn)行求解。對于表面裂紋前緣任意一點(diǎn)，將該點(diǎn)裂尖塑性區(qū)內(nèi)不同位置處垂直于裂紋面的拉伸應(yīng)力σyy與屈服強(qiáng)度σ0比值進(jìn)行平均，即得到約束因子α：
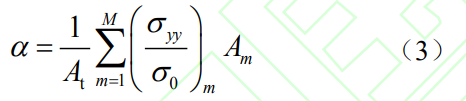
式中，m為裂紋前緣塑性區(qū)中單元編號，M為塑性區(qū)內(nèi)單元總數(shù)目，(σyy/σ0)m是塑性區(qū)內(nèi)裂紋面法向拉伸應(yīng)力與屈服應(yīng)力的比值，Am是單元m的面積，At是塑性區(qū)中所有單元的總面積。圖7給出了約束因子α的計(jì)算示意圖。
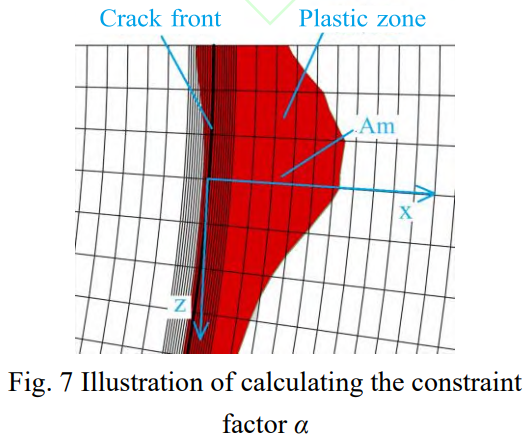
利用公式（3）對裂紋前緣不同位置的塑性區(qū)約束因子α進(jìn)行計(jì)算。考慮到計(jì)算過程復(fù)雜且算例數(shù)量較大，通過編制Abaquspythonscript后處理腳本實(shí)現(xiàn)上述計(jì)算過程。裂紋前緣不同位置使用歸一化弧度φ表示，φ從0到1表示裂紋前緣從一側(cè)與試樣表面交點(diǎn)位置到另一側(cè)與試樣表面交點(diǎn)位置，φ=0.5表示裂尖前緣位于試樣內(nèi)部最深位置。
3、結(jié)果與討論
3.1表面裂紋前緣應(yīng)力分布
圖8（a）為典型載荷下表面裂紋前緣彈塑性有限元分析結(jié)果，圖中灰白顏色區(qū)域表示裂尖塑性區(qū)，塑性區(qū)內(nèi)至少包含10個單元，驗(yàn)證了程序化網(wǎng)格劃分方法的有效性。裂尖塑性區(qū)呈現(xiàn)出試樣表面位置尺寸大、內(nèi)部位置尺寸小的特點(diǎn)。為進(jìn)一步深入分析，提取裂紋前緣裂紋面上塑性區(qū)的邊界，與裂紋前緣一同繪制，如圖8（b）所示。從圖中可見，裂紋面內(nèi)裂尖塑性區(qū)尺寸在試樣淺表層處達(dá)到最大，最外層表面處的塑性區(qū)尺寸略低于淺表層處尺寸；隨著裂紋前緣深度的增加，裂紋面內(nèi)塑性區(qū)尺寸迅速減少并逐漸穩(wěn)定，在最深點(diǎn)處達(dá)到最小尺寸。
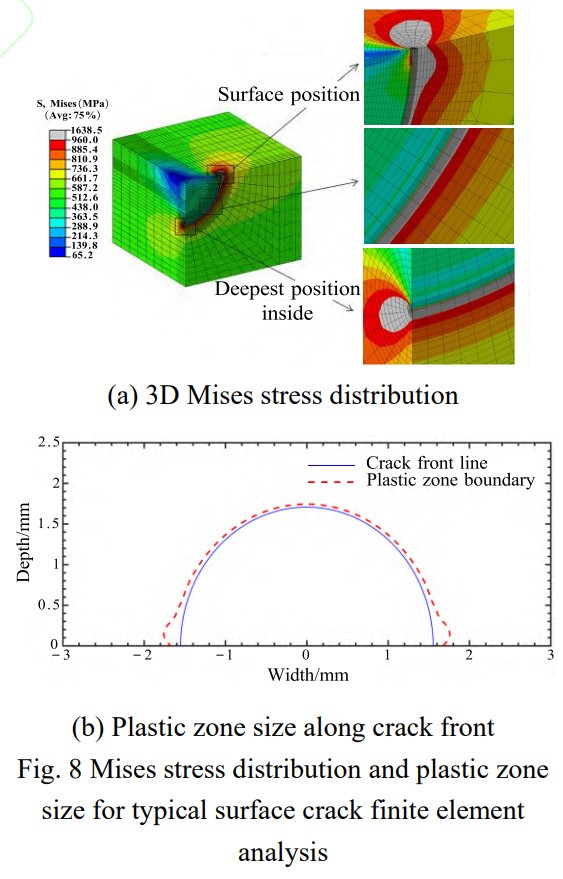
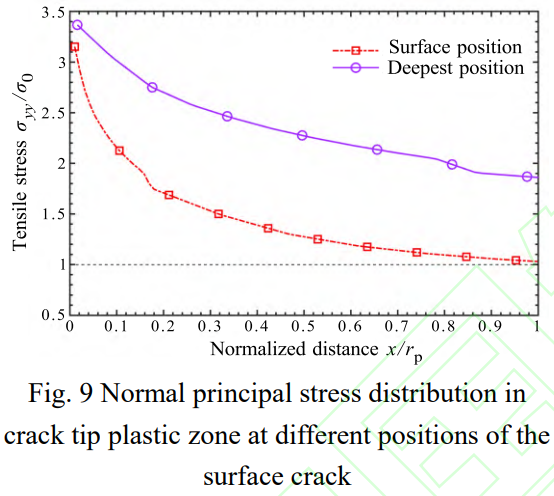
為了研究表面位置和內(nèi)部最深處裂紋前緣裂尖應(yīng)力場，提取相應(yīng)位置塑性區(qū)內(nèi)裂紋面拉伸應(yīng)力σyy/σ0隨到裂尖距離的分布曲線，如圖9所示。為便于比較，到裂尖距離通過相應(yīng)位置的塑性區(qū)尺寸rp進(jìn)行歸一化處理。圖中可見，表面和內(nèi)部最深處裂紋前緣裂紋面上的拉伸應(yīng)力隨到裂尖距離的增大均呈拋物線型分布，與Machniewicz等[24]研究結(jié)果一致。內(nèi)部最深處裂尖塑性區(qū)內(nèi)的拉伸應(yīng)力整體均大于表面位置裂尖塑性區(qū)內(nèi)拉伸應(yīng)力且下降趨勢更為緩慢，這是裂紋前緣不同位置約束作用不同導(dǎo)致的結(jié)果。
3.2表面裂紋前緣三維約束因子
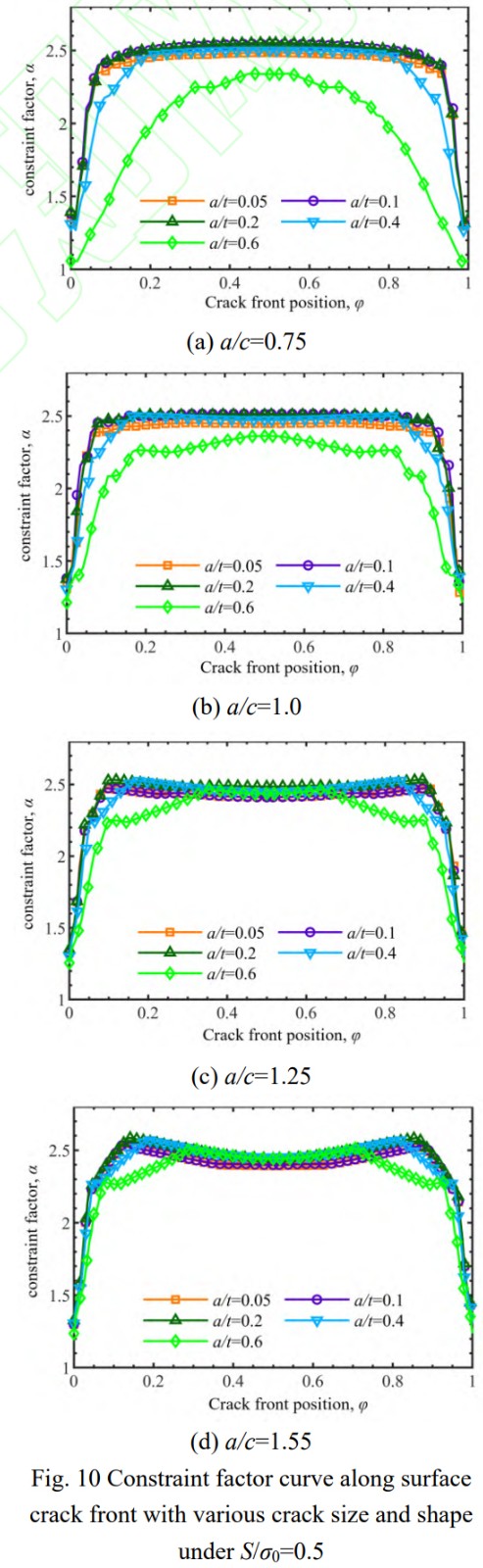
圖10給出了遠(yuǎn)場應(yīng)力S/σ0=0.5情況下，4種裂紋形狀（半軸比a/c=0.75，1.0，1.25，1.55），5種裂紋尺寸（裂紋厚度比a/t=0.05，0.1，0.2，0.4，0.6）表面裂紋前緣不同位置約束因子α分布情況。從圖中可以看出，α隨著裂紋前緣的位置變化近似呈“倒U型”，表面點(diǎn)處α數(shù)值在1.25左右，接近于平面應(yīng)力狀態(tài)。隨著裂紋前緣位置遠(yuǎn)離試樣表面，α迅速增大進(jìn)而趨向穩(wěn)定，最深處α數(shù)值在2.5左右，接近平面應(yīng)變狀態(tài)。相同裂紋形狀a/c下，當(dāng)裂紋相對尺寸a/t從0.05增大到0.4時，表面和最深處α變化相對較小，淺表層處則有較為明顯的下降；當(dāng)a/t繼續(xù)增大到0.6時，裂紋前緣不同位置處α均出現(xiàn)明顯下降。此時裂紋尺寸已大于試樣截面厚度一半，試樣整體約束作用顯著減小，進(jìn)而導(dǎo)致α整體下降。相同裂紋尺寸-試樣厚度比a/t下，當(dāng)半軸比a/c從0.75增大到1.55時，α整體變化不大，可見約束因子主要受表面裂紋深度方向最大尺寸影響。
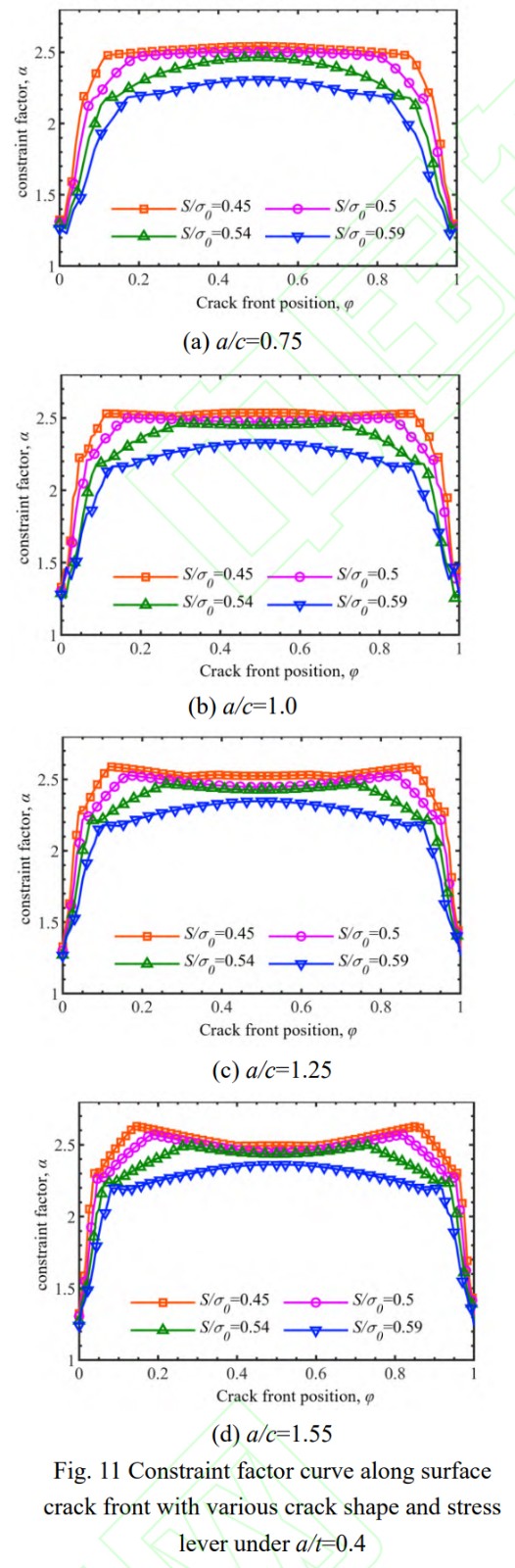
圖11為裂紋相對尺寸a/t=0.4時，不同應(yīng)力水平下（S/σ0=0.45，0.5，0.54，0.59），4種裂紋形狀（半軸比a/c=0.75，1.0，1.25，1.55）表面裂紋前緣不同位置約束因子分布情況。圖中可知，固定裂紋尺寸和形狀，隨著外加應(yīng)力水平的增大，表面點(diǎn)處α基本保持不變而最深點(diǎn)處的α有較為明顯的下降。此外，半軸比a/c=1.55情況下α隨載荷增大的下降幅度要小于半軸比a/c=0.75的情況。當(dāng)裂紋相對尺寸a/t保持不變時，a/c越大表示裂紋表面長度越�。豢梢�，裂紋尺寸較小時，α對載荷變化更不敏感。
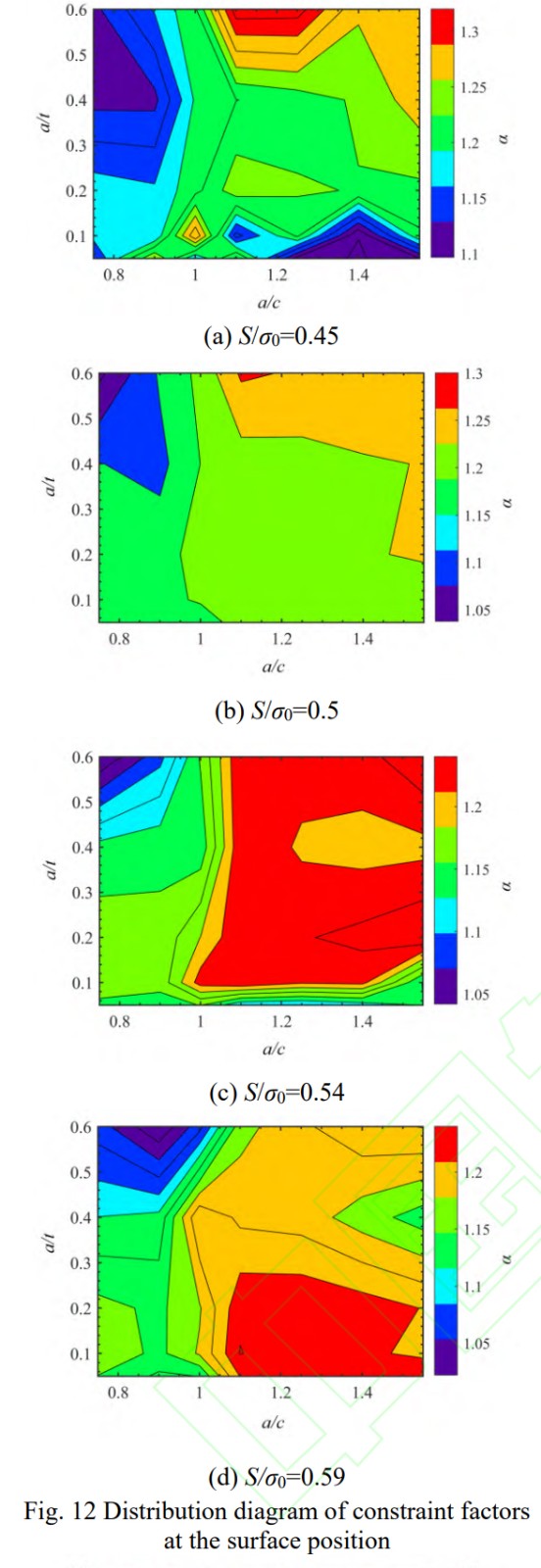
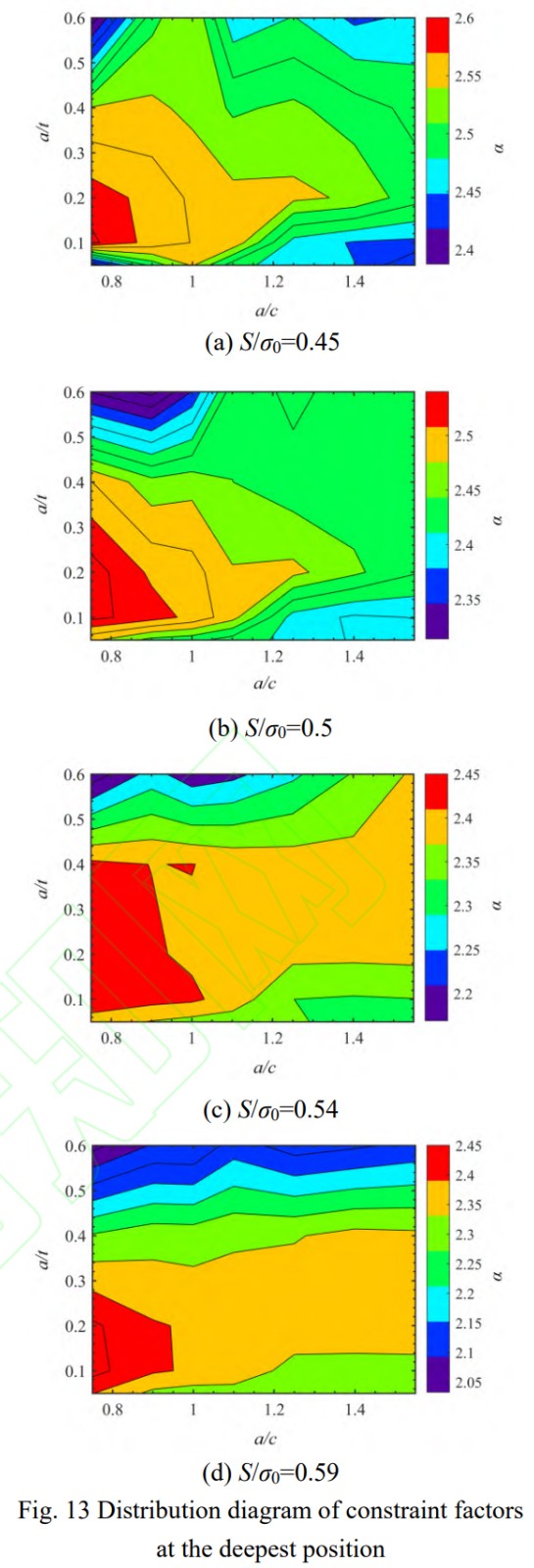
針對典型尺寸、形狀和應(yīng)力水平下的表面裂紋，分別提取表面位置和最深位置處的裂紋前緣α，繪制等值圖如圖12和圖13所示。對比兩圖可以發(fā)現(xiàn)，最深點(diǎn)處α隨裂紋尺寸和裂紋形狀變化的分布規(guī)律在不同加載水平下基本一致，最大值均分布在a/t=0.15，a/c=0.8附近；而表面點(diǎn)處α隨裂紋尺寸和裂紋形狀變化的分布規(guī)律在不同加載水平下有明顯差異：載荷水平較小時，α最大值出現(xiàn)在a/t=0.6，a/c=1.2附近；載荷水平較大時，α最大值出現(xiàn)在a/t=0.1，a/c=1.3附近。
3.3適用性分析
為分析本文提出的約束因子計(jì)算方法的適用性，與Guo方法進(jìn)行對比研究。Guo等[26]將有限厚板穿透裂紋中約束因子α的數(shù)值解與歸一化的平面應(yīng)力裂尖塑性區(qū)尺寸rp0/t相聯(lián)系，給出了約束因子計(jì)算公式：
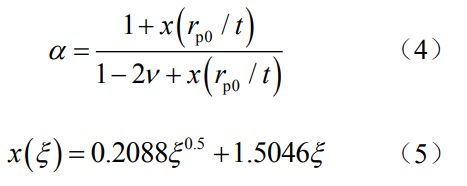
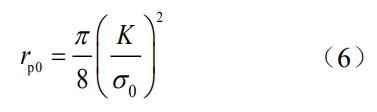
式中，rp0為加載時裂紋前緣裂紋面上塑性區(qū)尺寸，t為試樣厚度，ν為材料泊松比。進(jìn)一步地，于培師等[16-17]基于離面約束等效原則，通過表面裂紋前緣任一點(diǎn)處的離面約束參數(shù)Tz與厚度為Beq的中心穿透直裂紋厚度方向平均離面約束參數(shù)Tz相同的原則，將表面裂紋前緣上任一點(diǎn)處的約束狀態(tài)等效為一定厚度的中心穿透裂紋約束狀態(tài)。經(jīng)過系統(tǒng)分析表面裂紋前緣不同位置處Tz的分布，得到裂紋前緣線上弧度為φ的位置處等效厚度的擬合公式：
聯(lián)合式（4）~式（9），可以求得表面裂紋前緣上不同位置處的約束因子α值。
圖14給出了使用本文三維有限元分析方法得到的表面裂紋前緣最深點(diǎn)處約束因子與Guo方法計(jì)算的約束因子對比結(jié)果。
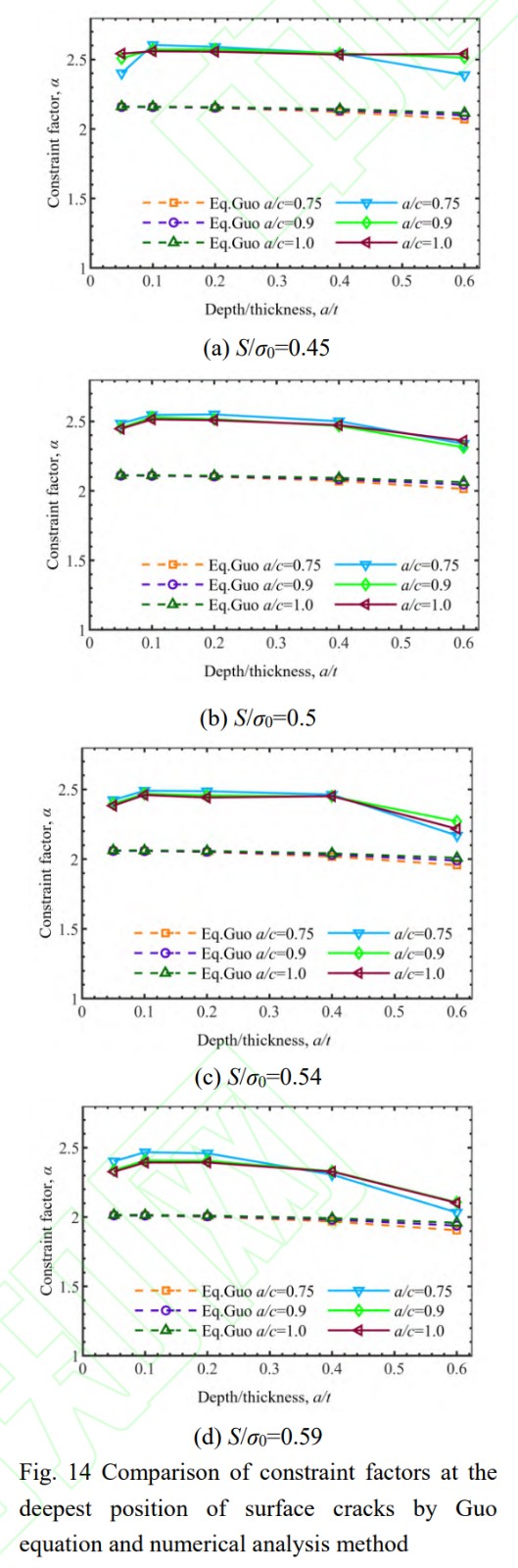
可以看到，Guo方法計(jì)算結(jié)果和本文有限元分析結(jié)果均能反映表面裂紋最深點(diǎn)處約束因子隨著載荷水平以及裂紋尺寸的增加總體呈減小趨勢。但Guo方法計(jì)算的約束因子值較本文有限元分析結(jié)果偏小，且隨a/t和a/c的變化趨勢不如本文有限元分析結(jié)果顯著。這可能是由于Guo方法通過厚度等效以及數(shù)據(jù)擬合等手段獲得了計(jì)算方程，存在一定的平均效果，而有限元數(shù)值仿真更能反映局部應(yīng)力、裂紋形狀以及材料特性的影響。此外，針對本文數(shù)值分析中出現(xiàn)了a/t較小時約束因子先增大在降低的現(xiàn)象，而Guo方法結(jié)果變化趨勢不明顯，說明本文方法能夠更好地反映表面裂紋尺寸和形狀綜合作用的影響。
針對表面位置處的約束因子，Guo方法根據(jù)式（7）和式（9）可以得到此處等效厚度Beq趨近0，因此約束因子α趨近1。而本文數(shù)值分析得到的裂紋表面點(diǎn)處約束因子在1~1.5，且隨a/t、a/c和S/σ0變化而變化�？梢姳疚奶岢龅臄�(shù)值方法能更好的反映不同裂紋尺寸、形狀和載荷水平下的裂紋前緣實(shí)際約束情況。此外，從式（7）可知，Guo方法僅給出了裂紋半軸比a/c≤1情況下的約束因子計(jì)算方法，本文數(shù)值方法則能進(jìn)一步考慮a/c>1的情況，具有更廣泛的裂紋形狀適用性。
上述對比研究表明，程序化仿真計(jì)算方法解決了裂紋前緣三維約束因子大量、快速計(jì)算的問題，同時具有精度高和適用性廣的特點(diǎn)。
4、結(jié)論
本文利用彈塑性有限元方法對發(fā)動機(jī)轉(zhuǎn)子用TC4鈦合金表面裂紋前緣三維約束因子分布特性進(jìn)行了研究，得到以下結(jié)論：
（1）表面裂紋前緣約束因子呈“倒U型”分布，從試樣表面位置到最深位置，約束效應(yīng)由近平面應(yīng)力狀態(tài)（α≈1.25）轉(zhuǎn)變?yōu)榻矫鎽?yīng)變狀態(tài)（α≈2.5）。裂紋表面點(diǎn)處約束因子隨著裂紋尺寸、裂紋形狀以及外加載荷的變化不明顯。裂紋最深點(diǎn)處約束因子隨外加載荷和裂紋尺寸的增大而減小，受裂紋形狀變化影響較小。等值線圖表明，裂紋前緣約束因子受裂紋尺寸、裂紋形狀以及外加載荷耦合作用，未表現(xiàn)出明顯的、單調(diào)的變化趨勢。
（2）對比研究了Guo方法和本文數(shù)值計(jì)算方法獲得的表面裂紋三維約束因子，結(jié)果表明有限元數(shù)值仿真更能反映局部應(yīng)力、裂紋形狀以及材料特性的影響，且能表征表面點(diǎn)處的約束因子分布。
在航空發(fā)動機(jī)鈦合金壽命限制件的疲勞裂紋擴(kuò)展研究中，可以利用本文建立的程序化分析方法，首先計(jì)算得到不同形狀和尺寸的裂紋前緣三維約束因子分布；然后結(jié)合疲勞裂紋閉合模型計(jì)算裂紋有效應(yīng)力強(qiáng)度因子范圍；進(jìn)而基于有效應(yīng)力強(qiáng)度因子范圍為驅(qū)動力的裂紋擴(kuò)展速率方程，進(jìn)行裂紋前緣不同位置處的擴(kuò)展預(yù)測；最終實(shí)現(xiàn)考慮三維裂紋前緣變約束效應(yīng)的航空發(fā)動機(jī)鈦合金轉(zhuǎn)子壽命限制件的裂紋擴(kuò)展壽命預(yù)測，并為最終的損傷容限評估提供支撐。
在后續(xù)的研究中，可進(jìn)一步開展不同材料、裂紋形狀和加載載荷下的約束因子計(jì)算分析，建立基礎(chǔ)數(shù)據(jù)庫，進(jìn)而發(fā)展基于數(shù)據(jù)驅(qū)動的快速、實(shí)用、高精度的計(jì)算模型，以便于在工程實(shí)踐中應(yīng)用。致謝：感謝國家自然科學(xué)基金和浙江省自然科學(xué)基金的資助。
參考文獻(xiàn)
[1] US Department of Transportation Federal Aviation Administration, Advisory Circular 33.70-1: Guidance material for aircraft engine-life-limited parts requirements[S], Washington DC, US, FAA, 2009.
[2] 中國民用航空局.航空發(fā)動機(jī)適航規(guī)定(CCAR-33R2) [S].北京：中國民用航空局, 2016.
[3] 丁水汀, 周惠敏, 劉俊博, 等. 航空發(fā)動 機(jī)限壽件表面特征概率損傷容限評估[J]. 航空動力學(xué)報, 2021,36(2):421-430.
DING S T, ZHOU H M, LIU J B, et al. Probabilistic damage tolerance assessment of surface features of aero engine life limited parts[J]. Journal of Aerospace Power, 2021,36(2):421-430. (in Chinese)
[4] DANIEWICZ S R. A modified strip-yield model for prediction of plasticity-induced closure in surface flaws[J]. Fatigue & Fracture of Engineering Materials & Structures, 1998(21):885-901.
[5] TORIBIO J, MATOS J C, GONZÁLEZ B. Aspect ratio evolution associated with surface cracks in sheets subjected to fatigue[J]. International Journal of Fatigue, 2016,92:588-595.
[6] TORIBIO J, MATOS J C, GONZÁLEZ B. Aspect ratio evolution in embedded, surface, and corner cracks in finite-thickness plates under tensile fatigue loading[J]. Applied Sciences, 2017,7(7):746.
[7] CORBANI S, CASTRO J T P, MIRANDA A C O, et al. Crack shape evolution under bending-induced partial closure[J]. Engineering Fracture Mechanics, 2018,188:493-508.
[8] ZHAO J H, GUO W L, SHE C M. Three-parameter approach for elastic-plastic fracture of the semi-elliptical surface crack under tension[J]. International Journal of Mechanical Sciences, 2008,50(7):1168-1182.
[9] ZHAO J H, GUO W L. Three-parameter KT-Tz characterization of the crack-tip fields in compact-tension-shear specimens[J]. Engineering Fracture Mechanics, 2012,92:72-88.
[10] CUI P F, GUO W L. Higher order J-T-A solution for three-dimensional crack border fields in power-law hardening solids[J]. Engineering Fracture Mechanics, 2019,222:106736.
[11] CUI P F, GUO W L. Crack-tip-openingdisplacement-based description of threedimensional elastic-plastic crack border fields[J]. Engineering Fracture Mechanics, 2020,231:107008.
[12] 郭萬林, 許磊, 周正. 三維計(jì)算斷裂力學(xué)[J]. 計(jì)算力學(xué)學(xué)報, 2016,33(4):431-440.
GUO W L, XU L, ZHOU Z. Computational mechanics of three-dimensional fracture[J]. Chinese Journal of Computational Mechanics, 2016,33(4):431-440. (in Chinese)
[13] WILLIAMS M L. On the stress distribution at the base of a stationary[J]. Journal of Applied Mechanics, 1957,24:109-114.
[14] O'DOWD N P. Applications of two parameter approaches in elastic-plastic fracture mechanics[J]. Engineering Fracture Mechanics, 1995,52(3): 445-465.
[15] GUO W L. Three-dimensional analyses of plastic constraint for through-thickness cracked bodies[J]. Engineering Fracture Mechanics, 1999,62(4):383-407.
[16] YU P S, GUO W L. An equivalent thickness conception for prediction of surface fatigue crack growth life and shape evolution[J]. Engineering Fracture Mechanics, 2012,93:65-74.
[17] YU P S, GUO W L. An equivalent thickness conception for evaluation of corner and surface fatigue crack closure[J]. Engineering Fracture Mechanics, 2013,99:202-213.
[18] ZHAO J H, GUO W L, SHE C M, et al. Three dimensional K-Tz stress fields around the embedded center elliptical crack front in elastic plates[J]. Acta Mechanica Sinica, 2006,22(2):148-155.
[19] GUO W, ZHU J C, GUO W L. Equivalent thickness-based three dimensional stress fields and fatigue growth of part-through cracks emanating from a circular hole[J]. Engineering Fracture Mechanics, 2020,228:106927.
[20] MOSTAFAVI M, SMITH D J, PAVIER M J. Reduction of measured toughness due to outof-plane constraint in ductile fracture of aluminium alloy specimens[J]. Fatigue & Fracture of Engineering Materials & Structures, 2010,33(11):724-739.
[21] YANG J. Unified correlation of constraint and strength mismatch with fracture toughness of bimetallic joint[J]. Procedia Engineering, 2015,130:853-860. [22] 徐建勇, 王國珍, 軒福貞,等. 基于裂尖張 開位移的統(tǒng)一拘束參數(shù)與材料斷裂韌性 的關(guān)聯(lián)[J]. 壓力容器, 2018,35(11):16-22.
XU J Y, WANG G Z, XUAN F Z, et al. Correlation of unified constraint parameter based on CTOD with fracture toughness of material[J]. Pressure Vessel Technology, 2018,35(11):16-22. (in Chinese) [23] NEWMAN J C. A crack-closure model for predicting fatigue crack growth under aircraft spectrum loading[M]. West Conshohocken, PA: ASTM International, 1981.
[24] MACHNIEWICZ T. Fatigue crack growth prediction models for metallic materials Part II: Strip yield model - choices and decisions[J]. Fatigue & Fracture of Engineering Materials & Structures,2013,36(4):361-373.
[25] NEWMAN J C, BIGELOW C A, SHIVAKUMAR K N. Three-dimensional elastic-plastic finite-element analyses of constraint variations in cracked bodies[J]. Engineering Fracture Mechanics, 1993, 46(1):1-13.
[26] GUO W L, WANG C K, ROSE L R F. The influence of cross-sectional thickness on fatigue crack growth[J]. Fatigue & Fracture of Engineering Materials & Structures, 1999,22(5):437-444. [27] WANG G S, BLOM A F. A strip model for fatigue crack growth predictions under general load conditions[J]. Engineering Fracture Mechanics, 1991,40(3):507-533.
[28] MCMASTER F J, SMITH D J. Predictions of fatigue crack growth in aluminium alloy 2024-T351 using constraint factors[J]. International Journal of Fatigue, 2001,23:93- 101.
[29] 吳連生, 于培師, 韋朋余, 等. 基于三維 理論的 TC4ELI 鈦合金疲勞裂紋擴(kuò)展研究[J]. 船舶力學(xué), 2022,26(9):1354-1362.
WU L S, YU P S, WEI P Y, et al. Fatigue crack growth of TC4ELI titanium alloy based on three-dimensional theory[J]. Journal of Ship Mechanics, 2022,26(9):1354-1362. (in Chinese)
[30] 許磊. 基于裂紋閉合模型的三維裂紋疲勞 擴(kuò)展分析[D].南京：南京航空航天大學(xué), 2018. XU L. Three-dimensional fatigue crack growth analysis based on crack closure model[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. (in Chinese)
[31] 周斌. 某鎳基粉末高溫合金三維裂紋擴(kuò)展 試驗(yàn)與分析研究[D].南京：南京航空航天 大學(xué), 2022.
ZHOU B. Experimental and analysis study on three-dimensional crack growth of a Nickel-base powder superalloy[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2022. (in Chinese)
[32] HUANG X N, CHEN C Y, XUAN H J. Experimental and analytical investigation for fatigue crack growth characteristics of an aero-engine fan disc[J]. International Journal of Fatigue, 2021,148:106252.
[33] MCCLUNG R C, LEVERANT G R, ENRIGHT M P, et al. Turbine Rotor Material Design: Phase II[R]. Washington, DC: Federal Aviation Administration, Department of Transportation, 2008.
[34] DANIEWICZ S R, AVELINE C R. Stripyield and finite element analysis of partthrough surface flaws[J]. Engineering Fracture Mechanics, 2000,67(1):21-39.
tag標(biāo)簽:鈦合金